python经典算法实践：平衡二叉树。分步图解平衡二叉树的插入过程
什么是 平衡二叉树 （balanced binary tree）
是一种特殊的 二叉排序树 ，它或者为空树，或者每个结点的左右子树都是平衡二叉树，也就是每个结点的左右子树的高度之差只能是-1,0,1三种情况。
平衡二叉树又称AVL树，是由苏联的Georgy Adelson-Velsky和E.M.Landis发明的，并以他们的名字命名。
平衡二叉树的平衡状况由平衡因子(Balance Factor,BF)来衡量。平衡因子定义为当前结点的左子树高度减去右子树的高度之差，其可能取值只有-1,0,1。叶结点的BF都是0
平衡二叉树的应用价值：
如果能维持平衡二叉树的结构，检索操作就能在O(log n)时间内完成，实现高效检索
最小不平衡子树：
距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树。（指BF超出合法值）
最小非平衡子树：
包含插入结点位置，其根结点的BF是1或-1的最小子树。（指BF非0，但BF在合法值范围内）
平衡二叉树-平衡因子BF取值
下图图一中，蓝色字体表示平衡二叉树对应节点的BF值
节点5的BF值 = 左边树的高度 – 右边数的高度 = 3-3=0，即BF = 0
节点4的BF值 = 左边树的高度 – 右边数的高度 = 1-0=1，即BF = 1
节点2的BF值 = 左边树的高度 – 右边数的高度 = 0-0=0，即BF = 0（即叶子节点BF=0）
节点8的BF值 = 左边树的高度 – 右边数的高度 = 0-1=-1，即BF = -1
节点10的BF值 = 0（叶子节点）
该 二叉树 所有节点的BF值在-1,0,1范围内，所以图一为平衡二叉树
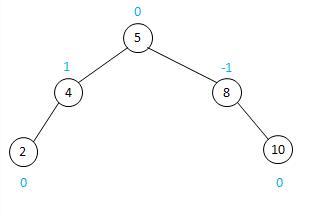
平衡二叉树-图1
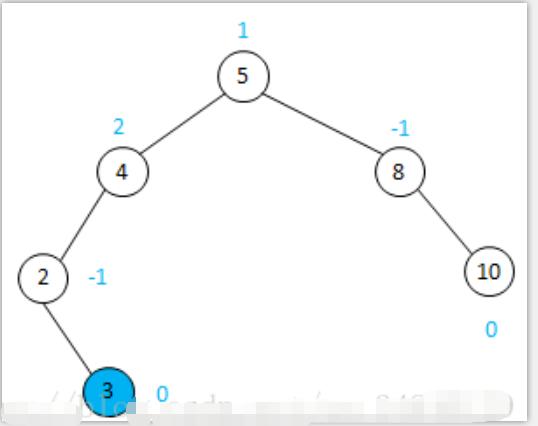
图二-平衡二叉树
图一的平衡二叉树插入元素3之后，如上图二
由于4节点的BF值 = 左边树的高度 – 右边数的高度 = 3-1=2，即BF =2，
BF值不在-1,0,1范围，故图二的二叉树不是平衡二叉树
无需调整：插入操作后仍是平衡二叉树
如下图三插入结点3，图四整棵树仍然是平衡的（各节点的BF值仍在-1,0，1范围）。
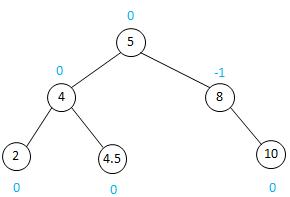
图三-平衡二叉树
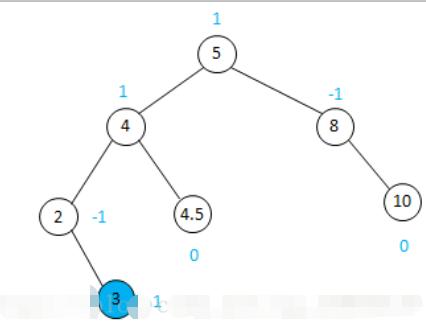
图四-平衡二叉树
LL型调整：a的左子树较高，新结点插入在a的左子树的左子树。进行右旋转。
在图五的图a中，a是最小非平衡子树的根，b的BF一定是0（否则a就不是最小非平衡子树的根了）。结点2被插入到了a的左子树的左子树，需要进行LL型调整：将结点2-3-4-5-8看做一条可以转动的链子，将其向右旋转（顺时针）一个结点，然后将原来b结点的右子树，接到a结点的左子结点上，调整完成。
图5-LL型调整-平衡二叉树
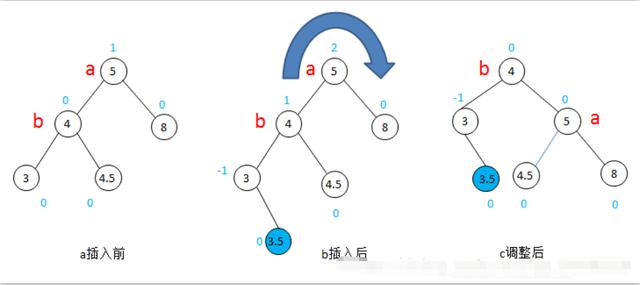
图6-LL型调整-平衡二叉树
插入新值后原来的平衡二叉树变成不平衡了，需要LL型调整，变成新的平衡二叉树。
LL型调整，需要右旋转， python 代码实现如下：
def LL(a, b): a.left = b.right # 将b的右子树接到a的左子结点上 b.right = a # 将a树接到b的右子结点上 a.bf = b.bf = 0 # 调整a、b的bf值。 return b
RR型调整：a的右子树较高，新结点插入在a的右子树的右子树。进行左旋转
RR型调整与LL型正好是对称的，操作步骤类似。
在下图（图7）的图a中，a是最小非平衡子树的根，b的BF一定是0。结点9被插入到了a的右子树的右子树，需要进行RR型调整：同样地，将结点4-5-6-8-9看做一条可以转动的链子，将其向左旋转（逆时针）一个结点，然后将原来b结点的左子树，接到a结点的右子结点上，调整完成。
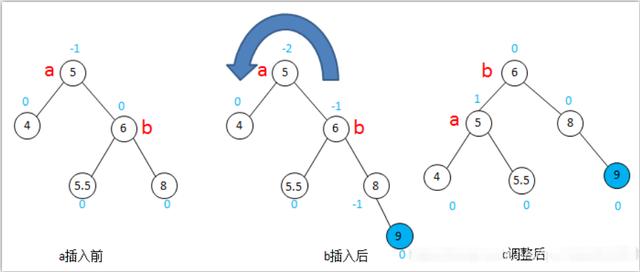
图7-RR型调整-平衡二叉树
同样地，插入结点也可以插入在结点8的左子结点处，调整步骤是一样的。
插入新值后原来的平衡二叉树变成不平衡了，需要RR型调整，变成新的平衡二叉树。
RR型调整，需要左旋转，python代码实现如下：
def RR(a, b): a.right = b.left b.left = a a.bf = b.bf = 0 return b
LR型调整：a的左子树较高，新结点插入在a的左子树的右子树。先进行左旋转，再进行右旋转
在下图（图8）的图a中，a是最小非平衡子树的根，b的BF一定是0，c的BF也一定是0。结点4.1被插入到了a的左子树的右子树（图b中4.1插入到了c结点的左子树，当然也可以插到c结点的右子树，其调整过程都是一样的），需要进行LR型调整。
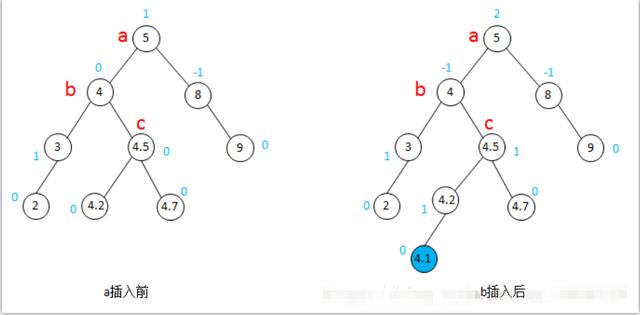
图8-LR型调整-平衡二叉树
在下图9种图c中，首先将c结点的左右子树分别摘下来，然后将结点4.5-4-3-2看做一条可以转动的链子，对其进行左旋转（逆时针）一个结点，就得到了图d，然后再将结点2-3-4-4.5-5-8-9看做一条转动的链子，将其进行右旋转（顺时针）一个结点，就得到了图e。
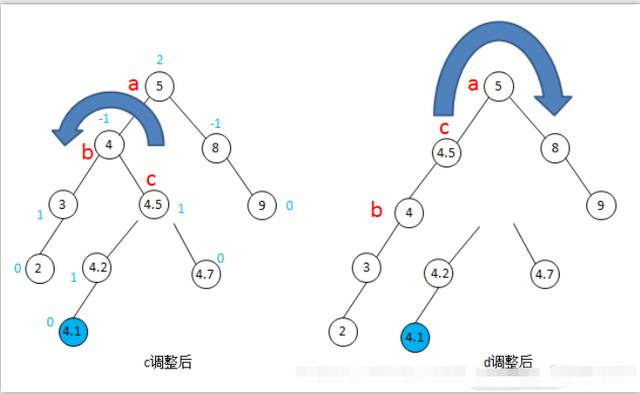
图9-LR型调整
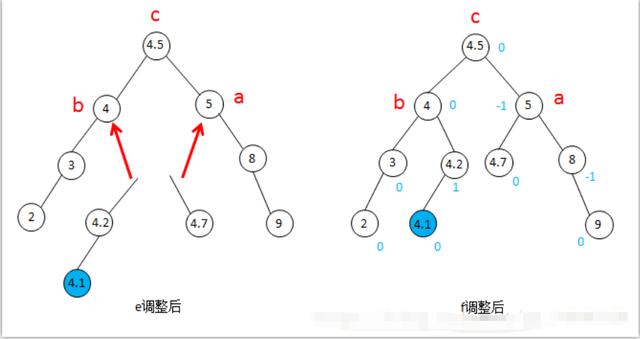
图10-LR型调整-平衡二叉树
最后将原来c结点的左子树接到b结点的右子结点上，将原来c结点的右子树接到a结点的左子结点上，调整完成。
插入新值后原来的平衡二叉树变成不平衡了，需要LR型调整，变成新的平衡二叉树。
LR型调整，python代码实现如下：
def LR(a, b): c = b.right a.left, b.right = c.right, c.left c.left, c.right = b, a if c.bf == 0: # c本身就是插入点 a.bf = b.bf = 0 elif c.bf == 1: # 插在c的左子树 a.bf = -1 b.bf = 0 else: # 插在c的右子树 a.bf = 0 b.bf = 1 c.bf = 0
RL型调整：a的右子树较高，新结点插入在a的右子树的左子树。先进行右旋转，再进行左旋转。
RL型调整与LR型正好是对称的，操作步骤类似。在下图的图a中，a是最小非平衡子树的根，b的BF一定是0，c的BF也一定是0。结点5.5被插入到了a的右子树的左子树（图b中5.5插入到了c结点的左子树，当然也可以插到c结点的右子树，其调整过程都是一样的），需要进行RL型调整。
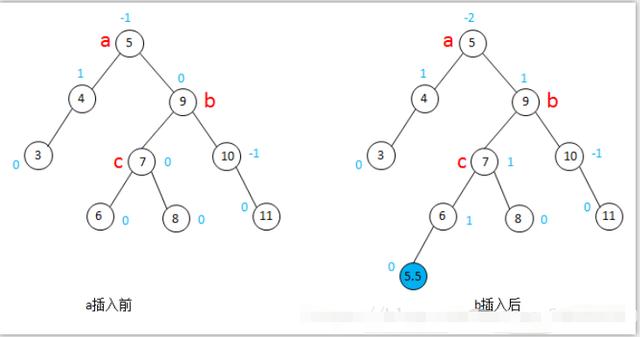
图11-RL型调整
在下图12中的图c中，首先将c结点的左右子树分别摘下来，然后将结点7-9-10-11看做一条可以转动的链子，对其进行右旋转（顺时针）一个结点，就得到了图d，然后再将结点3-4-5-7-9-10-11看做一条转动的链子，将其进行左旋转（逆时针）一个结点，就得到了图13中图e。
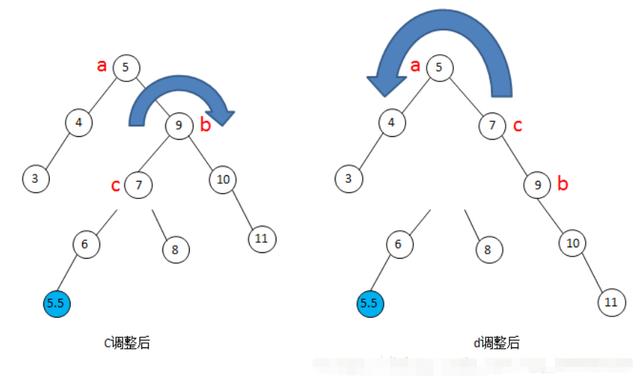
图12-RL型调整
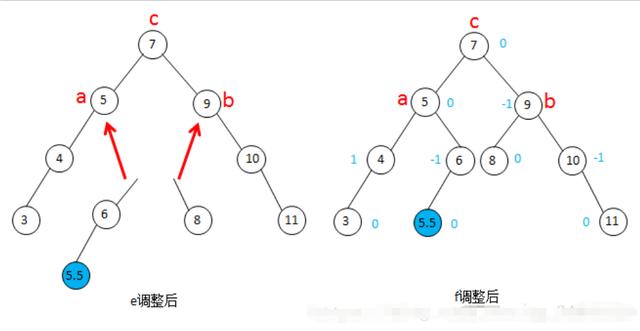
图13-RL型调整-平衡二叉树
最后将原来c结点的左子树接到a结点的右子结点上，将原来c结点的右子树接到b结点的左子结点上，调整完成。
插入新值后原来的平衡二叉树变成不平衡了，需要RL型调整，变成新的平衡二叉树。
RL型调整，python代码实现如下：
def RL(a, b): c = b.left a.right, b.left = c.left, c.right c.left, c.right = a, b if c.bf == 0: a.bf = b.bf = 0 elif c.bf == 1: a.bf = 0 b.bf = -1 else: a.bf = 1 b.bf = 0 c.bf = 0 return c
平衡二叉树的插入操作的复杂度是O(log n)
python用平衡二叉树来实现一个字典类
class StackUnderflow(ValueError):
pass
class SStack():
def __init__(self):
self.elems = []
def is_empty(self):
return self.elems == []
def top(self): # 取得栈里最后压入的元素，但不删除
if self.elems == []:
raise StackUnderflow('in SStack.top()')
return self.elems[-1]
def push(self, elem):
self.elems.append(elem)
def pop(self):
if self.elems == []:
raise StackUnderflow('in SStack.pop()')
return self.elems.pop()
class Assoc: # 定义一个关联类
def __init__(self, key, value):
self.key = key # 键（关键码）
self.value = value # 值
def __lt__(self, other): # Python解释器中遇到比较运算符<,会去找类里定义的__lt__方法（less than）
return self.key < other.key
def __le__(self, other): # （less than or equal to)
return self.key < other.key or self.key == other.key
def __str__(self):
return 'Assoc({0},{1})'.format(self.key, self.value) # key和value分别替换前面{0},{1}的位置。
class BinTNode:
"""
二叉树节点，数据，左节点，右节点
"""
def __init__(self, dat, left=None, right=None):
self.data = dat
self.left = left
self.right = right
class DictBinTree:
"""
二叉树类
"""
def __init__(self, root=None):
self.root = root
def is_empty(self):
return self.root is None
def search(self, key): # 检索是否存在关键码key
bt = self.root
while bt is not None:
entry = bt.data
if key < entry.key:
bt = bt.left
elif key > entry.key:
bt = bt.right
else:
return entry.value
return None
def insert(self, key, value):
bt = self.root
if bt is None:
self.root = BinTNode(Assoc(key, value))
return
while True:
entry = bt.data
if key < entry.key: # 如果小于当前关键码，转向左子树
if bt.left is None: # 如果左子树为空，就直接将数据插在这里
bt.left = BinTNode(Assoc(key, value))
return
bt = bt.left
elif key > entry.key:
if bt.right is None:
bt.right = BinTNode(Assoc(key, value))
return
bt = bt.right
else:
bt.data.value = value
return
def print_all_values(self):
bt, s = self.root, SStack()
while bt is not None or not s.is_empty(): # 最开始时栈为空，但bt不为空；bt = bt.right可能为空，栈不为空；当两者都为空时，说明已经全部遍历完成了
while bt is not None:
s.push(bt)
bt = bt.left
bt = s.pop() # 将栈顶元素弹出
yield bt.data.key, bt.data.value
bt = bt.right # 将当前结点的右子结点赋给bt，让其在while中继续压入栈内
def entries(self):
bt, s = self.root, SStack()
while bt is not None or not s.is_empty():
while bt is not None:
s.push(bt)
bt = bt.left
bt = s.pop()
yield bt.data.key, bt.data.value
bt = bt.right
def print_key_value(self):
for k, v in self.entries():
print(k, v)
def delete(self, key):
# 以下这一段用于找到待删除结点及其父结点的位置。
del_position_father, del_position = None, self.root # del_position_father是待删除结点del_position的父结点
while del_position is not None and del_position.data.key != key: # 通过不断的比较，找到待删除结点的位置
del_position_father = del_position
if key < del_position.data.key:
del_position = del_position.left
else:
del_position = del_position.right
if del_position is None:
print('There is no key')
return
if del_position.left is None: # 如果待删除结点只有右子树
if del_position_father is None: # 如果待删除结点的父结点是空，则说明待删除结点是根结点
self.root = del_position.right # 则直接将根结点置空
elif del_position is del_position_father.left: # 如果待删除结点是其父结点的左结点
del_position_father.left = del_position.right # ***改变待删除结点父结点的左子树的指向
else:
del_position_father.right = del_position.right
return
# 如果既有左子树又有右子树，或者仅有左子树时，都可以用直接前驱替换的删除结点的方式，只不过得到的二叉树与原理中说明的不一样，但是都满足要求。
pre_node_father, pre_node = del_position, del_position.left
while pre_node.right is not None: # 找到待删除结点的左子树的最右结点，即为待删除结点的直接前驱
pre_node_father = pre_node
pre_node = pre_node.right
del_position.data = pre_node.data # 将前驱结点的data赋给删除结点即可，不需要改变其原来的连接方式
if pre_node_father.left is pre_node:
pre_node_father.left = pre_ node .left
if pre_node_father.right is pre_node:
pre_node_father.right = pre_node.left
def build_dictBinTree(entries):
dic = DictBinTree()
for k, v in entries:
dic.insert(k, v)
return dic
class AVLNode(BinTNode):
def __init__(self, data):
BinTNode.___init__(self, data)
self.bf = 0
class DictAVL(DictBinTree):
def __init__(self, data):
DictBinTree.___init__(self)
@staticmethod
def LL(a, b):
a.left = b.right # 将b的右子树接到a的左子结点上
b.right = a # 将a树接到b的右子结点上
a.bf = b.bf = 0 # 调整a、b的bf值。
return b
@staticmethod
def RR(a, b):
a.right = b.left
b.left = a
a.bf = b.bf = 0
return b
@staticmethod
def LR(a, b):
c = b.right
a.left, b.right = c.right, c.left
c.left, c.right = b, a
if c.bf == 0: # c本身就是插入点
a.bf = b.bf = 0
elif c.bf == 1: # 插在c的左子树
a.bf = -1
b.bf = 0
else: # 插在c的右子树
a.bf = 0
b.bf = 1
c.bf = 0
return c
@staticmethod
def RL(a, b):
c = b.left
a.right, b.left = c.left, c.right
c.left, c.right = a, b
if c.bf == 0:
a.bf = b.bf = 0
elif c.bf == 1:
a.bf = 0
b.bf = -1
else:
a.bf = 1
b.bf = 0
c.bf = 0
return c
def insert(self, key, value):
a = p = self.root
if a is None: # 如果根结点为空，则直接将值插入到根结点
self.root = AVLNode(Assoc(key, value))
return
a_father, p_father = None # a_father用于最后将调整后的子树接到其子结点上
while p is not None: # 通过不断的循环，将p下移，查找插入位置，和最小非平衡子树
if key == p.data.key: # 如果key已经存在，则直接修改其关联值
p.data.value = value
return
if p.bf != 0: # 如果当前p结点的BF=0，则有可能是最小非平衡子树的根结点
a_father, a, = p_father, p
p_father = p
if key < p.data.key:
p = p.left
else:
p = p.right
# 上述循环结束后，p_father已经是插入点的父结点，a_father和a记录着最小非平衡子树
node = AVLNode(Assoc(key, value))
if key < p_father.data.key:
p_father.left = node
else:
p_father.right = node
# 新结点已插入，a是最小非平衡子树的根结点
if key < a.data.key: # 新结点在a的左子树
p = b = a.left
d = 1 # d记录新结点被 插入到a的哪棵子树
else:
p = b = a.right # 新结点在a的右子树
d = -1
# 在新结点插入后，修改b到新结点路径上各结点的BF值。调整过程的BF值修改都在子函数中操作
while p != node:
if key < p.data.key:
p.bf = 1
p = p.left
else:
p.bf = -1
p = p.right
if a.bf == 0: # 如果a的BF原来为0，那么插入新结点后不会失衡
a.bf = d
return
if a.bf == -d: # 如果新结点插入在a较低的子树里
a.bf = 0
return
# 以上两条if语句都不符合的话，说明新结点被插入在较高的子树里，需要进行调整
if d == 1: # 如果新结点插入在a的左子树
if b.bf == 1: # b的BF原来为0，如果等于1，说明新结点插入在b的左子树
b = DictAVL.LL(a, b)
else: # 新结点插入在b的右子树
b = DictAVL.LR(a, b)
else: # 新结点插入在a的右子树
if b.bf == -1: # 新结点插入在b的右子树
b = DictAVL.RR(a, b)
else: ##新结点插入在b的左子树
b = DictAVL.RL(a, b)
# 将调整后的最小非平衡子树接到原树中,也就是接到原来a结点的父结点上
if a_father is None: # 判断a是否是根结点
self.root = b
else:
if a_father == a:
a_father.left = b
else:
a_father.right = b
if __name__ == "__main__":
# LL调整
entries = [(5, 'a'), (2.5, 'g'), (2.3, 'h'), (3, 'b'), (2, 'd'), (4, 'e'), (3.5, 'f')]
dic = build_dictBinTree(entries)
dic.print_key_value()
print('after inserting')
dic.insert(1, 'i')
dic.print_key_value()
# LR调整
entries = [(2.5, 'g'), (3, 'b'), (4, 'e'), (3.5, 'f')]
dic = build_dictBinTree(entries)
dic.print_key_value()
print('after inserting')
dic.insert(3.2, 'i') # LL
dic.print_key_value()
最后，若有不正确之处，欢迎留言纠正
相关文章
本站已关闭游客评论，请登录或者注册后再评论吧~
热门文章
保利为什么叫央企之王(保利是国企还是央企)
2022-07-06
恢复外国人入境时间表(中国取消14天隔离政策了吗)
2021-06-19
香港哪些明星是反港分子(已背叛祖国的明星名单)被国家拉入黑名单明星
2021-04-20
身份造假与销售话术(记者卧底世纪佳缘 揭秘“红娘”)
2021-12-08
PyCharm怎么连接配置mysql数据库?
2021-06-29
如何将cda格式文件转换为mp3格式(cda格式怎么转换成mp3)
2021-12-11