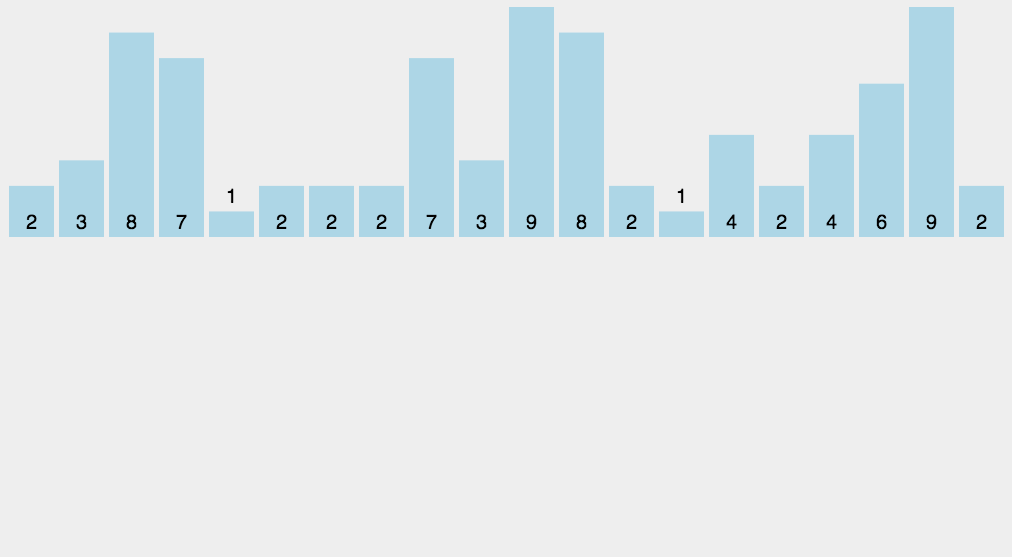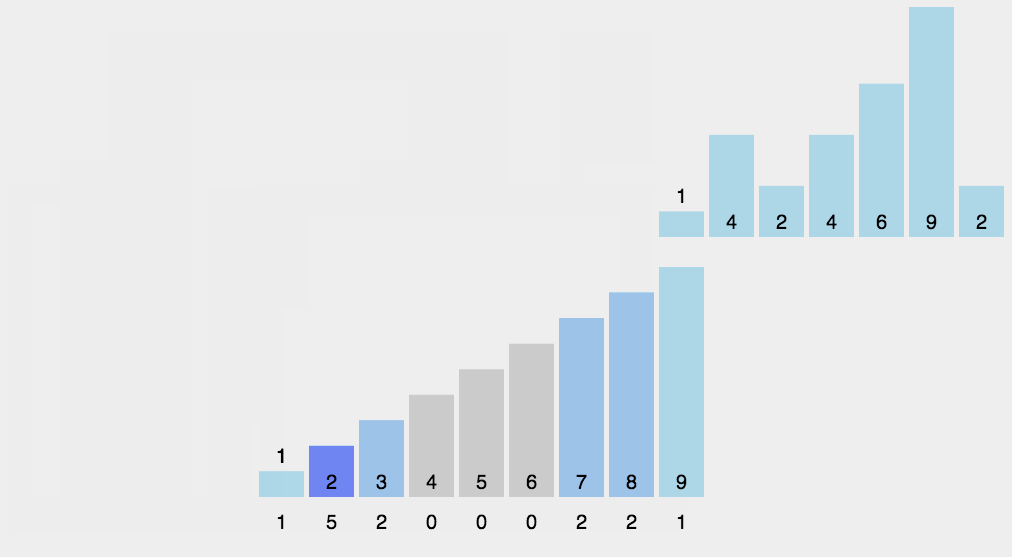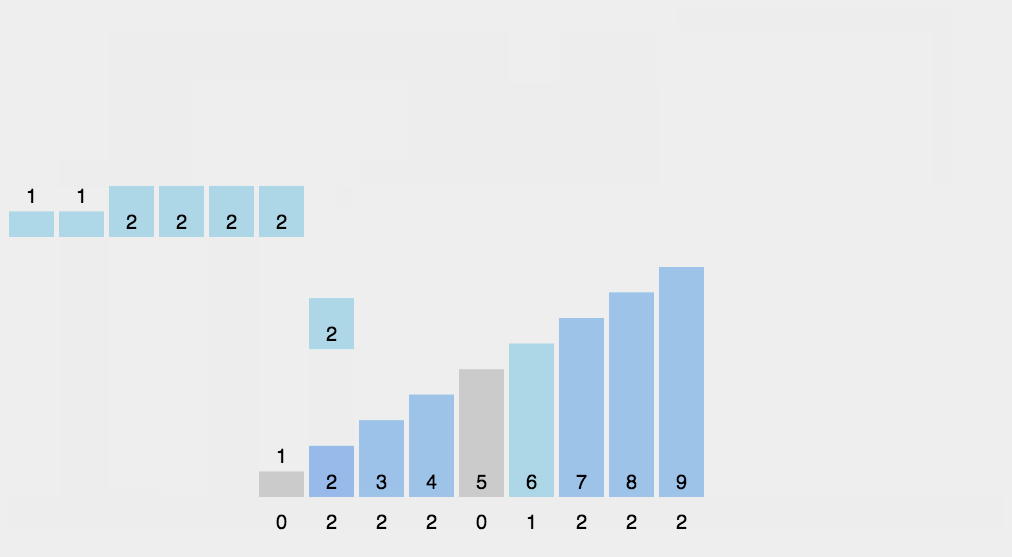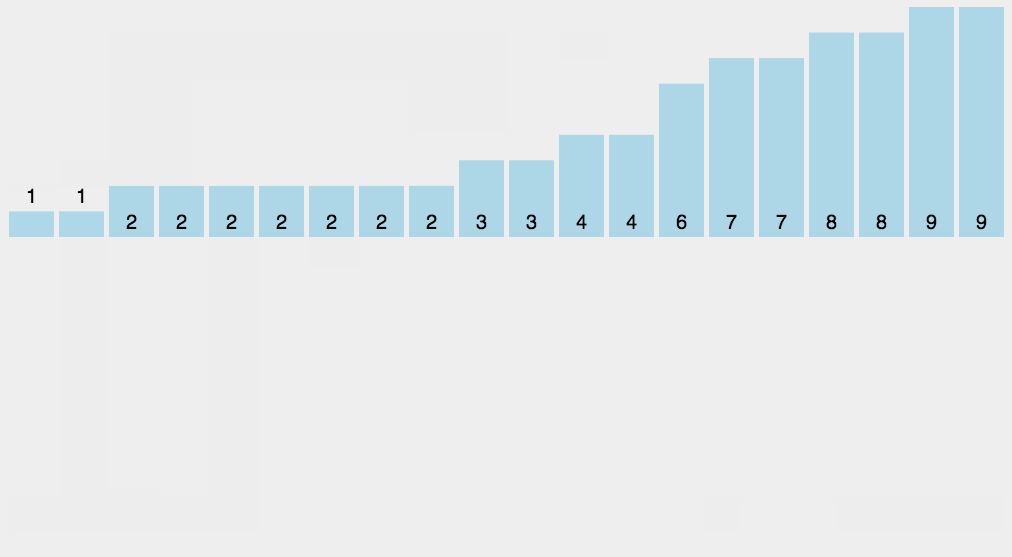导航

本文有点长,没错.是有点长

• 算法及解释

• 时间复杂度

• 数据结构和时间复杂度对比表

• JS实现

• PHP实现

算法及解释

百度百科中对于算法解释,我表示一脸懵逼.

算法分为5个步骤.有穷性(有限性)->确切性->输入->输出->可行性

浅显的解释就是: 我希望不费脑的读完这篇文章明白尽量多的知识(空间复杂度).或者快速读完这篇文章就完全明白作者讲的是什么(时间复杂度)

上面提到两个非常重要的概念.时间复杂度和空间复杂度.它是比较算法在你应用中适用与否选择的侧重点

如同本文.我们想要的结果是获得更多知识.这是评价文章好坏的结果.也是文章最终的结果(输出)

解释得越详细.你不管花多少时间就是需要明白.篇幅大占用的空间就大.这就是空间复杂度.因为你不在乎时间.

如果你在乎时间.那么文章篇幅必须小且精简.这就是时间复杂度

这是很逗比的解释.它当然不会那么简单.现在我要学习很多知识呢?比如JAVA,PHP,JS,甚至还想跟加藤鹰老师学习(有穷性(有限性)..你不可能什么都想学吧!)?那么相应的时间复杂度和空间复杂度就不是单一的线性表示,就需要一个公式来计算我到底需要多少时间才快速学习完这些知识(确切性..表示我学这些买一个步骤都是有意义,1+1=2).这里就不解释空间复杂度了,因为你的硬盘那么大,你会在乎电影多?

时间复杂度

指执行算法所需要的计算工作量。一般来说，计算机算法是问题规模n 的函数f(n)，算法的时间复杂度也因此记做 : T(n)=Ο(f(n))，问题的规模n 越大，算法执行的时间的增长率与f(n) 的增长率正相关.也称渐近时间复杂度，简称为时间复杂度，其中f(n) 是问题规模 n 的某个函数。

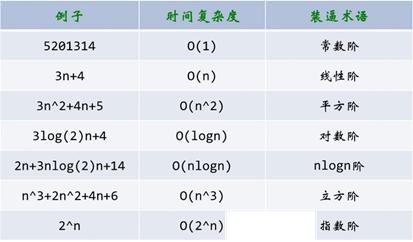
常见的时间复杂度

1.常数级复杂度 O(1)

2.对数级复杂度 O(logN)

3.线性级复杂度 O(n)

4.线性对数阶级复杂度 O(NlogN)

5.平方级复杂度 O(N^2)

6.立方O(N^3)

7.指数阶O(2^N)

时间复杂度所耗费时间从小到大依次是:

O(1) < O(logn) < (n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

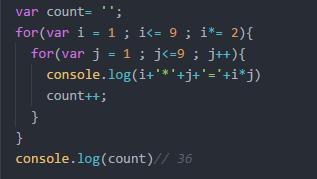
js 代码示例时间复杂度:

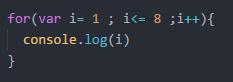
O(1) : 只执行了一次.比如数组查找 arr.apple或者arr[1]

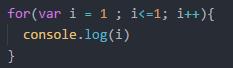
O(logN) 又或是O(log2N) : 执行了四次.比如二分结构算法将常数对分计算

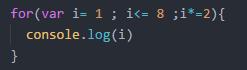
O(n) : 执行了八次.比如数组遍历

O(NlogN) : 循环内嵌套循环.

数据结构和时间复杂度对比表

常用数据结构的时间复杂度对比

数据结构	时间复杂度
	索引	查找	插入	删除	索引	查找	插入	删除
基本数组	O(1)	O(n)	–	–	O(1)	O(n)	–	–
动态数组	O(1)	O(n)	O(n)	O(n)	O(1)	O(n)	O(n)	O(n)
单链表	O(n)	O(n)	O(1)	O(1)	O(n)	O(n)	O(1)	O(1)
双链表	O(n)	O(n)	O(1)	O(1)	O(n)	O(n)	O(1)	O(1)
跳表	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(n)	O(n)	O(n)	O(n)
哈希表	–	O(1)	O(1)	O(1)	–	O(n)	O(n)	O(n)
二叉搜索树	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(n)	O(n)	O(n)	O(n)
笛卡尔树	–	O(log(n))	O(log(n))	O(log(n))	–	O(n)	O(n)	O(n)
B-树	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))
红黑树	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))
伸展树	–	O(log(n))	O(log(n))	O(log(n))	–	O(log(n))	O(log(n))	O(log(n))
AVL 树	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))

排序算法

算法	数据结构	时间复杂度	最坏情况下的辅助空间复杂度
		最佳	平均	最差	最差
快速排序	数组	O(n log(n))	O(n log(n))	O(n^2)	O(n)
归并排序	数组	O(n log(n))	O(n log(n))	O(n log(n))	O(n)
堆排序	数组	O(n log(n))	O(n log(n))	O(n log(n))	O(1)
冒泡排序	数组	O(n)	O(n^2)	O(n^2)	O(1)
插入排序	数组	O(n)	O(n^2)	O(n^2)	O(1)
选择排序	数组	O(n^2)	O(n^2)	O(n^2)	O(1)
桶排序	数组	O(n+k)	O(n+k)	O(n^2)	O(nk)
基数排序	数组	O(nk)	O(nk)	O(nk)	O(n+k)

堆

Heaps	时间复杂度
	建堆	查找最大值	提取最大值	Increase Key	插入	删除	合并
链表 （已排序）	–	O(1)	O(1)	O(n)	O(n)	O(1)	O(m+n)
链表（未排序）	–	O(n)	O(n)	O(1)	O(1)	O(1)	O(1)
二叉堆	O(n)	O(1)	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(m+n)
二项堆	–	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))
斐波那契堆	–	O(1)	O(log(n))*	O(1)*	O(1)	O(log(n))*	O(1)

图

节点 / 边 管理	Storage	Add Vertex	Add Edge	Remove Vertex	Remove Edge	Query
邻接表	O(|V|+|E|)	O(1)	O(1)	O(|V| + |E|)	O(|E|)	O(|V|)
关联表	O(|V|+|E|)	O(1)	O(1)	O(|E|)	O(|E|)	O(|E|)
邻接矩阵	O(|V|^2)	O(|V|^2)	O(1)	O(|V|^2)	O(1)	O(1)
关联矩阵	O(|V| ⋅ |E|)	O(|V| ⋅ |E|)	O(|V| ⋅ |E|)	O(|V| ⋅ |E|)	O(|V| ⋅ |E|)	O(|E|)

搜索

算法	数据结构	时间复杂度	空间复杂度
		平均	最差	最差
深度优先搜索 (DFS)	Graph of |V| vertices and |E| edges	-	O(|E| + |V|)	O(|V|)
广度优先搜索 (BFS)	Graph of |V| vertices and |E| edges	-	O(|E| + |V|)	O(|V|)
二分查找	Sorted array of n elements	O(log(n))	O(log(n))	O(1)
穷举查找	Array	O(n)	O(n)	O(1)
最短路径-Dijkstra，用小根堆作为优先队列	Graph with |V| vertices and |E| edges	O((|V| + |E|) log |V|)	O((|V| + |E|) log |V|)	O(|V|)
最短路径-Dijkstra，用无序数组作为优先队列	Graph with |V| vertices and |E| edges	O(|V|^2)	O(|V|^2)	O(|V|)
最短路径-Bellman-Ford	Graph with |V| vertices and |E| edges	O(|V||E|)	O(|V||E|)	O(|V|)

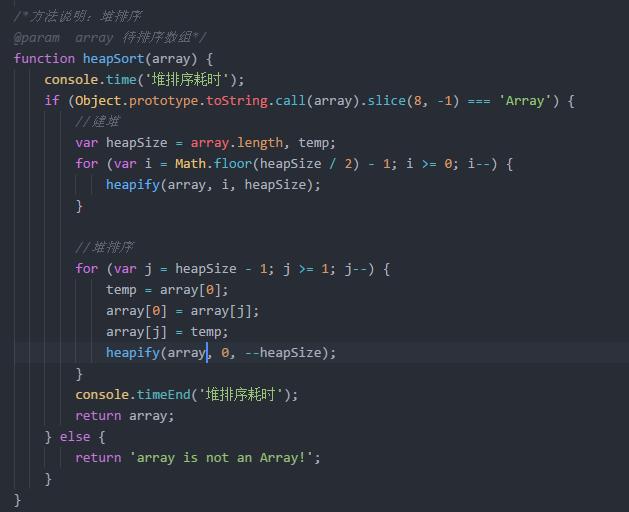
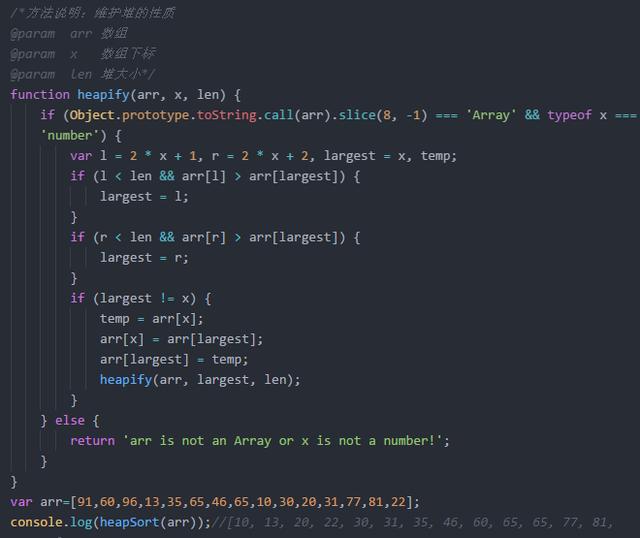
JS实现

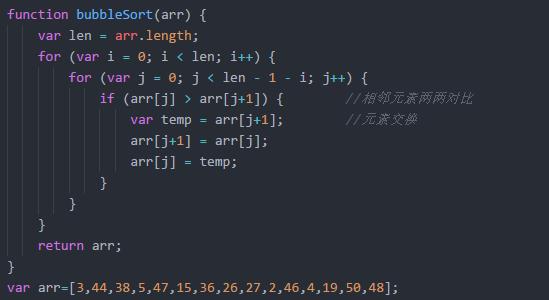
冒泡排序

遍历排列的数列.依次比较两个元素.如果顺序错误(左小右大为正确)就把他们交换过来.不停遍历到不需要交换为止(数列已经排序完成,越小的数会不停交换浮现到数组左边)

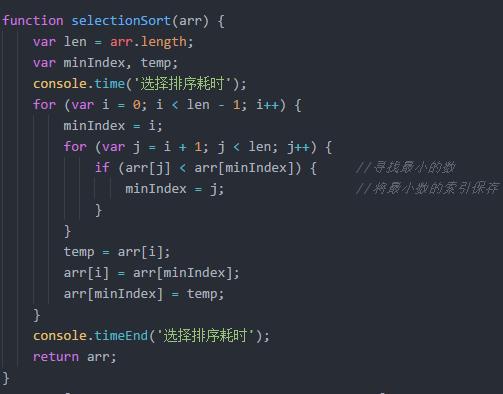
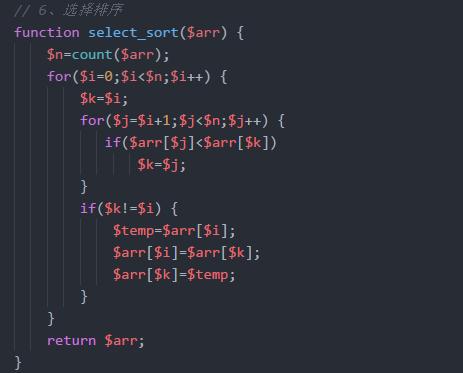
选择排序

在未排序的数列中找到最小(或大)放在排序序列的开始(或结束)位置.然后从剩下的序列中继续寻找最小(或大)元素,放到已经排序的序列中末尾.直到所有元素排列完成.适用于数据规模小的排序算法.因为任何数据都是O(N2)的时间复杂度,好处就是不占用额外内存

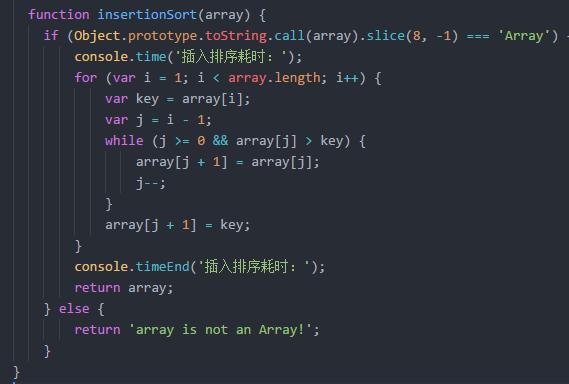
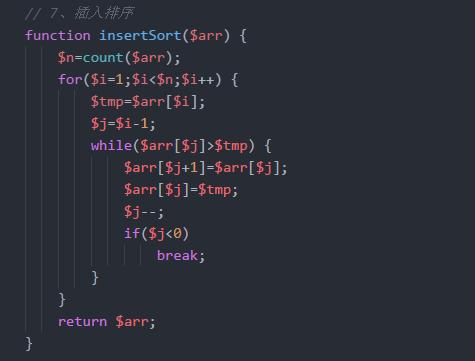
插入排序

通过构建有序序列.对于未排序数据.在已排序序列向前扫描.找到相应位置并插入.插入排序在实现上采用in-place排序(只需要用到O(1)的额外空间排序),因而在向前扫描中,需要反复把已排序元素向后挪位.为新元素提供插入位置

希尔排序

核心在于间隔序列的设定.即可用提前设定好间隔序列,也可以动态定义间隔序列.希尔排序的简单插入排序的改进版,他和排序不同之处在于他会优先比较较远的元素.希尔排序又叫缩小增量排序

解释: 根据增量值跳过序列来进行对比.增量初始化值应该合理分配(小则分配小.大分配大).

算法分析 : 突破了O(n^2)的排序算法.因为根据动态增量来跳过数列.类似于二分排序

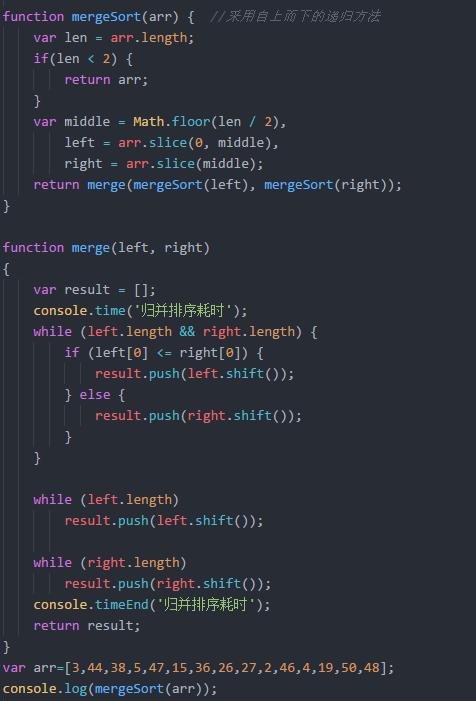
归并排序

归并采用分治法,归并是一种稳定算法,将已经有序的子序列合并,得到完全有序的序列.即先使每个子序列有序再将有序列合并,称为2路归并.归并排序性能不受输入数据影响,但表示比选择排序好,始终都是O(NlonN)的时间复杂度.代价是额外内存.即空间复杂度

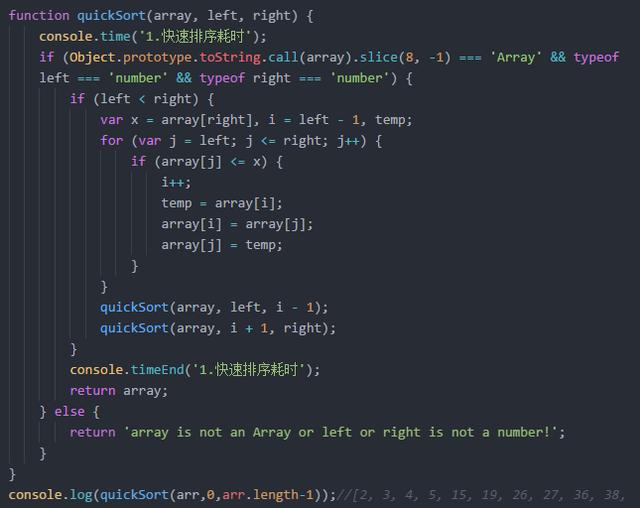
快速排序

通过一次排序将待排序记录分隔成独立两部分,其中一部分的数据均比另一部分小.则可分别对这两部分记录继续进行排序.以达到整个序列有序.是最快的排序方法

堆排序

利用堆这种数据结构设计的一种排序算法.堆积是一个近似完全二叉树的结构,并同时满足堆积的性质: 即子结点的键值或索引总是小于（或者大于）它的父节点。

计数排序

计数排序是一种稳定算法.使用一个额外数组C,其中第i个元素是数组A待排序数组中等于i元素的个数,然后根据数组C将A中的元素排到正确位置,它只能对整数且数值必须有确定范围的数组排序

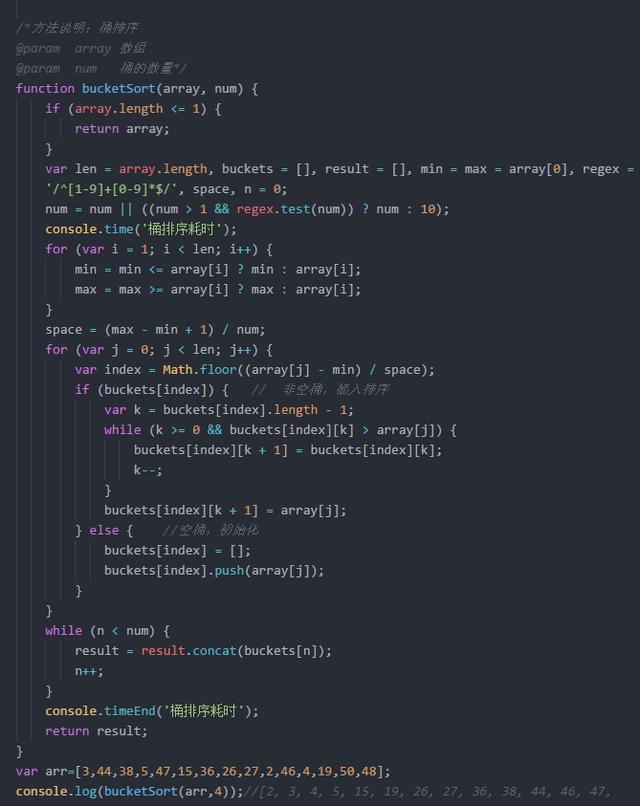
桶排序

桶排序假设输入数据均匀分布.将数据分到有限的桶里.将桶里的数据分别进行排序(可以是任何算法或递归调用).桶排序是计数排序的升级版,它使用函数的映射关系.高效与否在于函数映射的确定

解释: 比如存在数组 [ 1,2,2,5]

那么会创建5个桶(依赖数组中最大数).[0,1,2,3,4,5].在采用计数算法表示.[0,1,2,0,0,1].因为存在1和2个2和5.下标就是这样表示在遍历出来即可

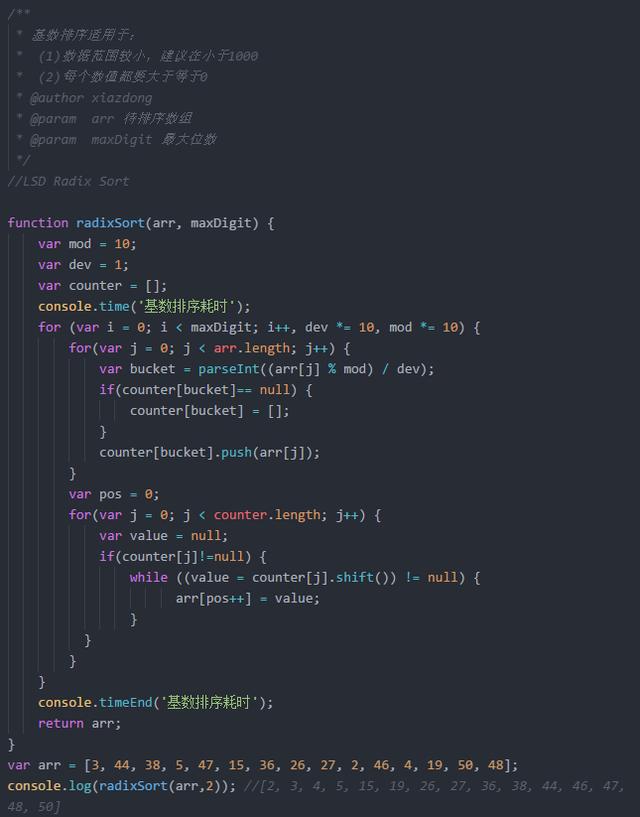
基数排序

基数排序是按照低位先排序.然后收集.再按照高位排序.再收集.以此类推.直到最高位.有些属性是有优先级顺序的,先按低优先级排序再排序高优先级.

基数排序基于分别排序.分别收集.所以是稳定的.基数排序也是非比较的的排序算法.从低位开始,复杂度为O(kn).k为数组中最大位数

适用于数据范围小的数组

PHP实现

---

总结 :

算法是前辈们的呕心沥血.更是数学在计算中的精粹.请尊重程序员.PHP是世界上最好的语言~