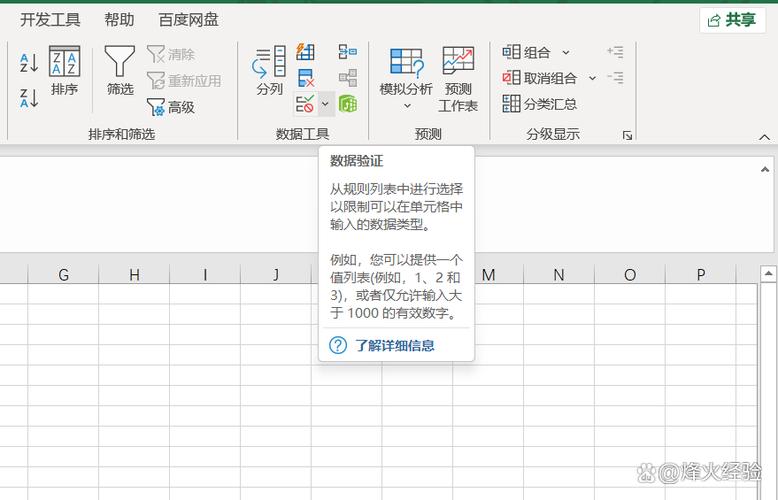
七年级10道简单趣味数学题？(十道趣味数学题)

1.有人编写了一个程序,从1开始,交替做乘法或加法,（第一次可以是加法,也可以是乘法）,每次加法,将上次运算结果加2或是加3；每次乘法,将上次运算结果乘2或乘3,例如30,可以这样得到十道趣味数学题：1 +3 =4*2=8+2=10*3=30,请问怎样可以得到：2的100次+2的97次-2

1+3=4+2=2的3次-2=2的3次+2-2=（2的3次+2-2）*2=……==2的100次+2的97次-2的97次=2的100次+2的97次-2的97次+2=2的100次+2的97次-2的97次+2+2=……=2的100次+2的97次-2

2.下诗出于清朝数学家徐子云的著作,请算出诗中有多少僧人?

巍巍古寺在云中,不知寺内多少僧.

三百六十四只碗,看看用尽不差争.

三人共食一只碗,四人共吃一碗羹.

请问先生明算者,算来寺内几多僧?

三人共食一只碗：则吃饭时一人用三分之一个碗,

四人共吃一碗羹：则吃羹时一人用四分之一个碗,

两项合计,则每人用1/3+1/4=7/12个碗,

设共有和尚X人,依题意得：

7/12X=364

解之得,X=624

3.两个男孩各骑一辆自行车,从相距2O英里（1英里合1.6093千米）的两个地方,开始沿直线相向骑行.在他们起步的那一瞬间,一辆自行车车把上的一只苍蝇,开始向另一辆自行车径直飞去.它一到达另一辆自行车车把,就立即转向往回飞行.这只苍蝇如此往返,在两辆自行车的车把之间来回飞行,直到两辆自行车相遇为止.如果每辆自行车都以每小时1O英里的等速前进,苍蝇以每小时15英里的等速飞行,那么,苍蝇总共飞行了多少英里?

每辆自行车运动的速度是每小时10英里,两者将在1小时后相遇于2O英里距离的中点.苍蝇飞行的速度是每小时15英里,因此在1小时中,它总共飞行了15英里.

4.《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料.下卷收集了一些算术难题,“鸡兔同笼”问题是其中之一.原题如下：令有雉（鸡）兔同笼,上有三十五头,下有九十四足.问雄、兔各几何?

设x为雉数,y为兔数,则有

x＋y＝b,2x＋4y＝a

解之得：y＝b／2－a,

x＝a－（b／2－a）

根据这组公式很容易得出原题的答案：兔12只,雉22只.

5.我们大家一起来试营一家有80间套房的旅馆,看看知识如何转化为财富.

经调查得知,若我们把每日租金定价为160元,则可客满；而租金每涨20元,就会失去3位客人.每间住了人的客房每日所需服务、维修等项支出共计40元.

问题：我们该如何定价才能赚最多的钱?

日租金360元.

虽然比客满价高出200元,因此失去30位客人,但余下的50位客人还是能给我们带来360*50=18000元的收入； 扣除50间房的支出40*50=2000元,每日净赚16000元.而客满时净利润只有160*80-40*80=9600元.

6、两名自行车运动员,相距60KM,他们同时以10KM/小时的速度向对方驶去,一只鸟儿从其中一名运动员这边飞了出来,以25KM\\小时的速度向另一名运动员飞去,等它与另一名运动员相遇后又飞回第一名运动员身边.它一只这样飞来飞去.那么,最后小鸟飞行的总距离是多少?

解 运动员3小时后相遇,小鸟飞了3小时,25乘以3,=75KM.

7、4个人过桥,大哥5分钟,二哥10分钟,三弟25分钟,四弟25分钟,现在是午夜,他们只有一个手电筒,所以过了桥的人还要把手电筒送回来,怎样才能在半小时内全部过桥?

解 大哥和二弟先过,大哥送回手电筒,三弟和四弟过,二弟送回手电筒,二弟和大哥一起过,一共1小时.

十道趣味数学题要答案，字数少。。。。

手工制作课上，小红利用一些花布的边角料，剪裁后装饰手工画，下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边，其中，每个图案花边的宽度都相等，那么，每个图案中花边的内外边缘所围成的几何图形不相似的是 如图，等腰△ ABC中，AB=AC，∠A=20°。线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于A、80° B、 70° C、60° D、50° 如图，直线y1=k1x+a与y2=k3x+b的交点坐标为（1,2），则使y1∠ y2的x的取值范围为A、x＞1 B、x＞2 C、x＜1 Dx＜211、如图，△ ABC内接于⊙O，D为线段AB的中点，延长OD交⊙O于点E，连接AE，BE，则下列五个结论①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤ ,正确结论的个数是A、2 B、3 C、4 D、512、如图，AB为半圆的直径，点P为AB上一动点，动点P从点A出发，沿AB匀速运动到点B，运动时间为t，分别以AP于PB为直径做半圆，则图中阴影部分的面积S与时间t之间的函数图像大致为第2卷二、填空题（本题共6个小题，每小题4分，满分24分）13、在函数y= ，自变量x的取值范围是__________。14、在如图所示的矩形纸片上作随机扎针实验，则针头扎在阴影区域的概率为________。 15、方程x2-2x-1=0的两个实数根分别为x1，x2，则（x1-1）（x1-1）=_________。16、将两张矩形纸片如图所示摆放，使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上，则∠1+∠2=_____________。17、计算 -2sin60°+(π-1)2=_____________________。18、如图，在平面直角坐标系中，点O为原点，菱形OABC的对角线OB在x轴上，顶点A在反比例函数y= 的图像上，则菱形的面积为____________。三、解答题（本大题共8各小题，满分78分）19、（本题满分6分）先简化，再求值： 其中 20、（本题满分10分）如图，在平面直角坐标系中，△ ABC的三个顶点的坐标分别为A（0,1），B（-1,1），C（-1,3）。（1）画出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；（2）画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2，并写出点C2的坐标；，（3）将△A2B2C2平移得到△ A3B3C3，使点A2的对应点是A3，点B2的对应点是B3 ，点C2的对应点是C3（4，-1），在坐标系中画出△ A3B3C3，并写出点A3，B3的坐标。 21、（本题满分8分）在烟台市举办的“读好书、讲礼仪”活动中，东华学校积极行动，各班图书角的新书、好书不断增多，除学校购买外，还有师生捐献的图书，下面是七年级（1）班全体同学捐献图书的情况统计图：请你根据以上统计图中的信息，解答下列问题：（1）该班有学生多少人？（2）补全条形统计图；（3）七（1）班全体同学所卷图书的中位数和众数分别是多少？ 22、（本题满分8分）小刚很擅长球类运动，课外活动时，足球队、篮球队都力邀他到自己的阵营，小刚左右为难，最后决定通过掷硬币来确定。游戏规则如下：连续抛掷硬币三次，如果三次正面朝上或三次反面朝上，则由小刚任意挑选两球队；如果两次正面朝上一次正面朝下，则小刚加入足球阵营；如果两次反面朝上一次反面朝下，则小刚加入篮球阵营。（1）用画树状图的方法表示三次抛掷硬币的所有结果。（2）小刚任意挑选两球队的概率有多大？（3）这个游戏规则对两个球队是否公平？为什么？ 23、（本题满分8分）去冬今春，我国西南地区遭遇历史上罕见的旱灾，解放军某部接到了限期打30口水井大的作业任务，部队官兵到达灾区后，目睹灾情心急如焚，他们增派机械车辆，争分夺秒，每天比原计划多打3口井，结果提前5天完成任务，求原计划每天打多少口井？ 24、（本题满分10分）如图以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点D恰好为BC的中点，过点D作⊙O的切线交AC边于点E。（1）求证：DE⊥AC；（2）若∠ABC=30°，求tan∠BCO的值。25、（本题满分14分）如图，△ABC中AB=AC,BC=6,点D位BC中点，连接AD，AD=4,AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为E。（1）试判断四边形ADCE的形状并说明理由。（2）将四边形ADCE沿CB以每秒1个单位长度的速度向左平移，设移动时间为t（0≤t≤6）秒，平移后的四边形A’D’C’E’与△ABC重叠部分的面积为S，求S关于t的函数表达式，并写出相应的t的取值范围。 26、（本题满分14分）如图，已知抛物线y=x2+bx-3a过点A（1,0），B(0,-3),与x轴交于另一点C。（1）求抛物线的解析式；（2）若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，求点P的坐标；（3）在（2）的条件下，在抛物线上是否存在一点Q，使以P,Q,B,C为顶点的四边形为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由。

/zhanzheng/a04/000.htm

以上就是三问网网»十道趣味数学题，七年级10道简单趣味数学题？的相关内容了，更多精彩请关注三问网号公众号。