培养孩子想象力最好的方法(空间想象力如何提高)
在数学学习过程中,很多人不怕解题训练的繁琐,不怕知识定理的记忆,更不怕压轴题的挑战,但偏偏输给一些特殊技能的培养,如空间想象力。
要想学好数学,特别是对于几何内容来说,一个人在几何的道路上能走多远,很大程度上取决于空间想象力。
那么,什么是空间想象力呢?
一般情况下,我们把对客观事物的空间形式或空间几何形体,进行观察、分析、认知、研究等的抽象思维能力,就称之为空间想象力。
简而言之就是我们通过观察某一空间几何形体,如某一立体几何图,分析和研究其中点、线、面、角等元素之间的关系,再转化成具体的数学语言,从而帮助我们解决问题。
一个人能否通过观察和分析几何形体得到相关的“信息量”(即空间想象力),而这些“信息量”将成为你解决问题的关键所在。因此,在中小学教育阶段,一直把空间想象力的培养作为数学教育的主要目标之一。
很多人花费大量的时间和精力,在课外寻找提升空间想象力的方法或策略,其实这是一种南辕北辙的学习方法,得不偿失,因为在我们的数学课本里就安排了培养和提高空间想象力的学习内容,如三视图的学习。
三视图能很好培养学生的空间想象能力,与其他数学内容相比,可以帮助我们从不同的角度观察几何体所看到的平面图形,是了解几何体特性的重要途径之一。因此,通过三视图的学习和考查,更有利于培养和发展学生的空间观念。
三视图一般包括主视图(也叫做正视图)、俯视图和左视图这三大部分。
培养学生空间想象力,方法1:
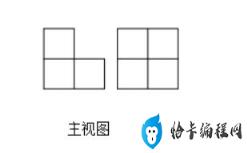
一个几何体是由一些大小相同的小正方体摆成的,其主视图与左视图如图所示,则组成这个几何体的小正方体最少有 个。
解:综合左视图和主视图,这个几何体的底层最少有2+1=3个小正方体,
第二层最少有2个小正方体,
因此组成这个几何体的小正方体最少有3+2=5个,
故答案为5.
考点分析:
由三视图判断几何体、图表型。
题干分析:
根据三视图的知识,主视图是由3个小正方形组成,而左视图是由4个小正方形组成,故这个几何体的底层最少有3个小正方体,第2层最少有2个小正方体.
解题反思:
本题考查了由几何体判断三视图,题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就容易得到答案.
培养学生空间想象力,方法2:
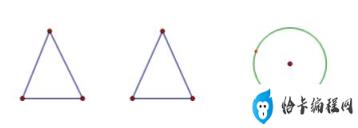
如图是一个几何体的三视图,则这个几何体的名称是 。
解:根据三视图的知识,主视图以及左视图都是三角形,
俯视图为圆形,故可判断出该几何体是圆锥;
故答案为圆锥.
考点分析:
由三视图判断几何体、作图题。
题干分析:
根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
解题反思:
本题考查了由判断几何体,解题的关键是正确的利用其三个视图的形状作出判断。
在平时学习过程中,很多学生为什么没能在三视图的学习中提高空间想象能力呢?经过调查研究发现,这些学生都是按照传统的学习方式学习三视图,如都只是通过刷题和多解题等,脱离实际生活,没有充分利用图片和实物模型,在思维能力培养上出现断层。
培养学生空间想象力,方法3:
如图,一个小立方块所搭的几何体,从不同的方向看所得到的平面图形中(小正方形中的数字表示在该位置的小立方块的个数),不正确的是( )
解:左视图中的每个数字是该位置小立方体的个数,分析其中的数字,得主视图有3行,从左到右的列数分别是1,4,2.故选B.
考点分析:
简单组合体的三视图。
题干分析:
分别得到该物体的三视图中的每个行列中的正方形的个数后找到错误的即可。
解题反思:
本题考查了简单组合体的三视图,考查了同学们的空间想象能力,本题灵活考查了三种视图之间的关系以及视图和实物之间的关系,同时还考查了对图形的想象力。
三视图不仅是重要的学习内容,也是近些年中高考数学的热点,特别是由一些相同的小正方体组成的几何体的三视图的试题是近几年全国各地中高考数学常考题型之一。
培养学生空间想象力,方法4:
下列几何体各自的三视图中,只有两个视图相同的是( )
解:①正方形的主、左和俯视图都是正方形;
②圆锥的主、左视图是三角形,俯视图是圆;
③球体的主、左和俯视图都是圆形;
④圆柱的主、左视图是长方形,俯视图是圆;
只有两个视图相同的几何体是圆锥和圆柱.
故选D.
考点分析:
简单几何体的三视图、应用题。
题干分析:
分别分析四个几何体的三视图,从中找出只有两个视图相同的几何体,可得出结论.
解题反思:
本题考查了几何体的三视图,熟练掌握常见几何体的三视图,考查了学生的空间想象能力.
一个人的空间想象力强不强,主要看以下三个方面的内容:
一是能根据空间几何形体或根据表述几何形体的语言、符号,在大脑中展现出相应的空间几何图形,并能正确想象其直观图;
二是能根据直观图,在大脑中展现出直观图表现的的几何形体及其组成部分的形状、位置关系和数量关系;
三是能对头脑中已有的空间几何形体进行分解、组合,产生新的空间几何形体,并正确分析其位置关系和数量关系。
简单的讲就是考查识图、画图的能力、运算求解能力等基本能力。
培养学生空间想象力,方法5:
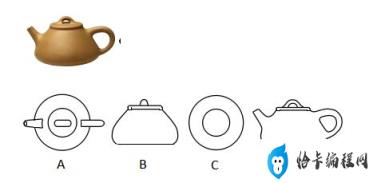
从不同方向看一只茶壶,你认为是俯视效果图的是( )
解:选项A的图形是从茶壶上面看得到的图形.故选A.
考点分析:
简单组合体的三视图.
题干分析:
俯视图就是从物体的上面看物体,从而得到的图形;找到从上面看所得到的图形即可.
解题反思:
本题考查了三视图的知识,明确一个物体的三视图:俯视图就是从物体的上面看物体,从而得到的图形.
学好三视图,提高空间想象力,关键一点是要在观察、比较、想象、综合、抽象分析的过程中,大家要主动去探索空间几何形体,积极与老师或同学合作交流,这样对你的空间观念的培养能起到很大的帮助。
培养学生空间想象力,方法6:
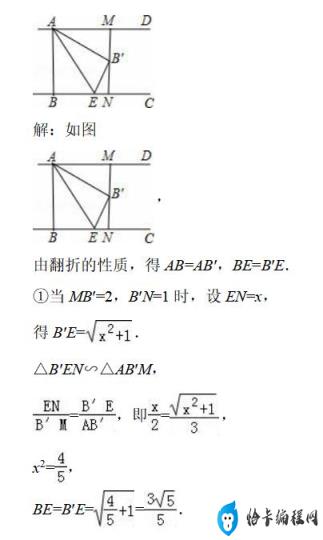
如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为 .
考点分析:
翻折变换(折叠问题).
题干分析:
根据勾股定理,可得EB′,根据相似三角形的性质,可得EN的长,根据勾股定理,可得答案.
解题反思:
本题考查了翻折的性质,利用翻折的性质得出AB=AB′,BE=B′E是解题关键,又利用了相似三角形的性质,要分类讨论,以防遗漏。
通过三视图的学习,学会把一个立体图形抽象成平面图形,或是把平面图形还原成立体图形,把立体的图形具体化和平面化,达到由未知到已知,由抽象到具体的转化,这样就能很好的培养和发展学生的空间观念和空间想象能力。
同时,在处理三视图相关问题的过程中,能够帮助学生学会从不同的侧面,不同的角度对几何体的结构特征进行认识和加工,提高分析问题和解决问题的能力,锻炼思维能力,培养探索创新能力等。