子集和真子集的区别(子集和真子集举例)
子集和真子集的区别,子集和真子集举例。发迹号带你了解更多相关信息。高中数学的开始就是学习集合,因为集合最简单,和初中联系最为紧密。所以我经常说,学习是一个环,每一环都要严丝合缝,学的深入,理解透彻,否则,越到后面,越是遇到变化的题型,别人可
子集和真子集的区别,子集和真子集举例。发迹号带你了解更多相关信息。
高中数学的开始就是学习集合,因为集合最简单,和初中联系最为紧密。所以我经常说,学习是一个环,每一环都要严丝合缝,学的深入,理解透彻,否则,越到后面,越是遇到变化的题型,别人可以做到举一反三,你做不到,甚至看不懂题问是是什么,这就是为什么提问是最能了解学生到底学会了没有最有效的方式。
值得注意的是,孩子在学校,每次都被老师提问的概率是比较小的,所以如果家长有时间和专业能力,可以适当的跟孩子进行提问,就当是亲子互动啦,也是很有意思的一件事哦。
如果家长没时间或者没有专业知识,可以请学校老师多多关注自家孩子。或者请一位专门的家庭教师,专业的事情让专业的人做,省时有效。
对于子集和真子集的区分,最简单有效的区分方法就是举例子说明,并记住这个例子,而不是去背诵它们的概念!!!
如果集合A的任意一个元素都是集合B的元素(任意a∈A则a∈B),那么集合A称为集合B的子集,记为A⊆B或 B⊇A,读作“集合A包含于集合B”或集合B包含集合A”。即:∀a∈A有a∈B,则A⊆B。
真子集 如果集合A是B的子集,且A≠B,即B中至少有一个元素不属于A,那么A就是B的真子集,可记作:A⊊B。符号语言:若∀a∈A,均有a∈B,且x∈B使x∉A,则A⊊B。百度搜索
这里要讲一下学习的误区,有同学背诵各个概念背的非常熟悉,可以一做题就是不会,根本原因就是孩子的学习思维还停留在小学!小学的语文、数学、英语这三门,为什么很多孩子可以考接近满分呢?一方面是因为题型简单(相对于初中生和高中生来说),另一方面也是起决定性作用的因素是小学的内容量小,所以考法简单,题型固定,就算小孩子不理解,凭借背诵能力和大量的练习就可以做到接近满分。所以小学的学习思维是背诵,只要背会就行。但是初中,高中,只背会,不理解,这样做一定是学不会的,而且孩子很心累,我明明很努力,为什么成绩还是不进步,陷入自我怀疑之中,怀疑自己脑子笨,不适合学习,反正也学不会,干脆不听了吧,越不听越不会,陷入恶性循环。
初中的学习量、题型变化比起小学多了不止几倍,几十倍都不为过。高中比起初中更是如此。
所以,人们才说,高考是人生的再一次生命。在经历了小学6年,初中3年,高中3年的认真学习之后,大部分高考生都掌握了必考的而且不变的题型,可以过二本线。学校同年级所有学生中,每次考试成绩总在前30%的高考生,幸运的话,可以上普通一本,超常发挥,可以上名校一本。至于北大、清华这些顶级学校,大概率会降临在那个每次都是年级第一名的身上。说回正题,集合中子集和真子集的区别和联系是什么呢?
举个例子(如果你不懂这个知识点,请记住这个例子,理解之后,遇到题目套用就可以了)。给定集合A=
一,B跟A完全相同,B是A的子集。B=
画个图表示就是
二,去掉A中的任意一个元素之后构成的集合是A的子集。B=
去掉A中的任意几个元素之后构成的集合是A的子集。B= 画个图表示就是
三,完全去掉A中的全部元素之后构成的集合是A的子集。空集。
结论汇总:
所以,含有n个元素的集合,有 2的n次方个子集。所以,含有n个元素的集合,有 2的n次方-1 个真子集。所以,含有n个元素的集合,有 2的n次方-1 个非空子集。所以,含有n个元素的集合,有 2的n次方-2 个非空真子集。
理解了子集的概念之后,再看真子集就简单多了。真子集就是:给定集合A=去掉A中的任意一个元素之后构成的集合是A的真子集。B=
去掉A中的任意几个元素之后构成的集合是A的真子集。B= 画个图表示就是
完全去掉A中的全部元素之后构成的集合是A的真子集。空集。
结论汇总:
含有n个元素的集合,有 2的n次方个子集。含有n个元素的集合,有 2的n次方-1 个真子集。含有n个元素的集合,有 2的n次方-1 个非空子集。含有n个元素的集合,有 2的n次方-2 个非空真子集。
如果你还是觉得好多内容,那么请你一定记住这三个图和这两句话。
子集:
或者
空集是任何集合的子集。真子集:
空集是任何非空集合的真子集。
推荐阅读
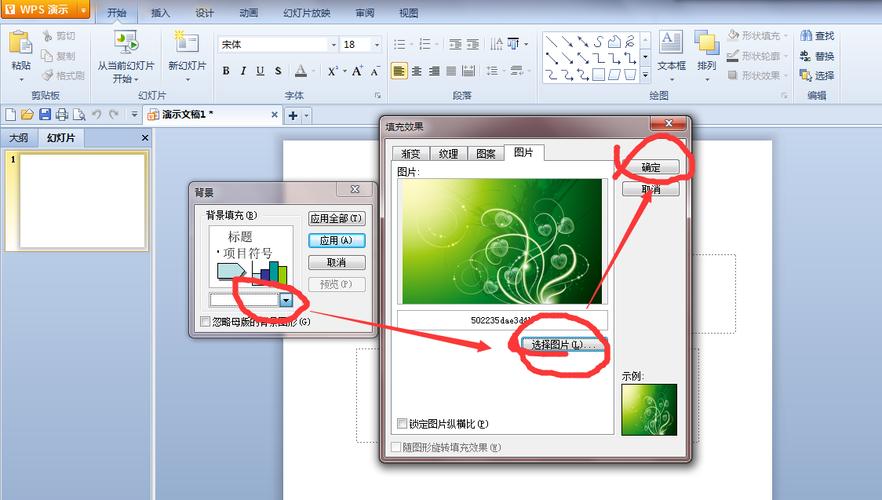
如何在PPT中插入背景图片?3步操作详解
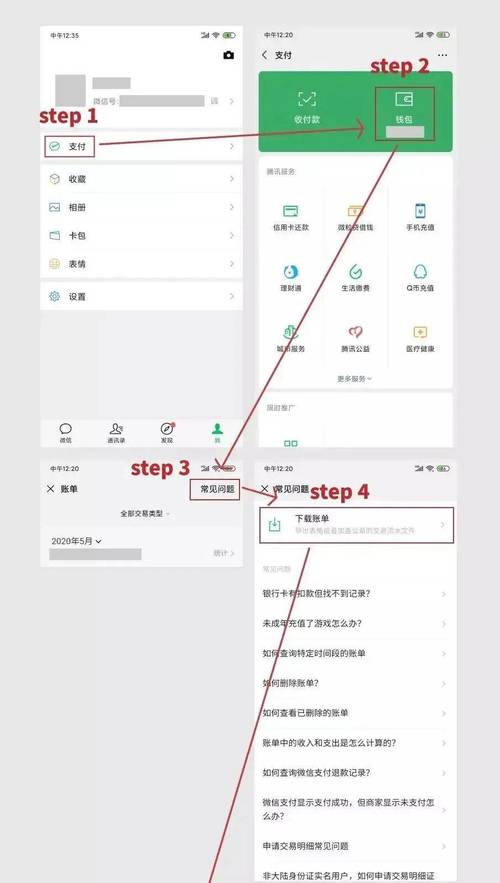
微信能直接转账到支付宝吗?如何实现跨平台转账?
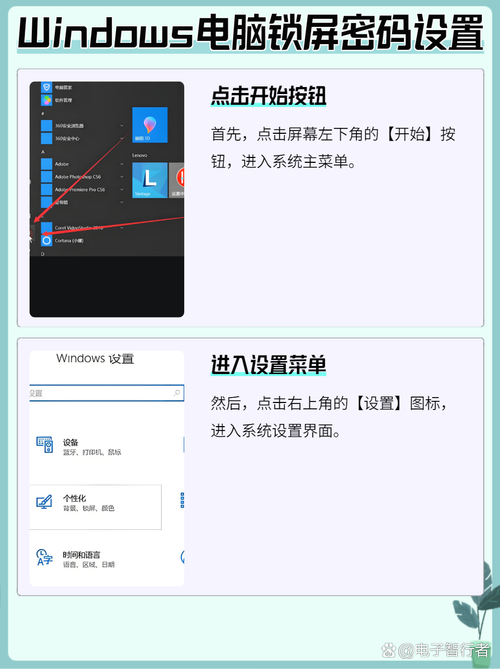
电脑锁屏如何设置?Windows与Mac系统操作步骤详解
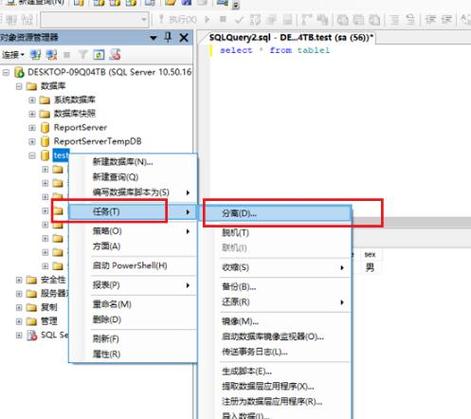
如何打开MDF文件?推荐工具与操作步骤

如何将A4纸打印成一半大小?简单步骤解析

如何改变思维模式?有效方法与实用步骤
如何设置有效性规则,分步指南与最佳实践
微信如何换行打字?手机和电脑版正确方法
如何将PDF转换成Excel?简单步骤解析
如何查看电脑日志?简单步骤与工具推荐

如何在PPT中插入背景图片?3步操作详解

微信能直接转账到支付宝吗?如何实现跨平台转账?

电脑锁屏如何设置?Windows与Mac系统操作步骤详解

如何打开MDF文件?推荐工具与操作步骤

如何将A4纸打印成一半大小?简单步骤解析

如何改变思维模式?有效方法与实用步骤

如何设置有效性规则,分步指南与最佳实践

微信如何换行打字?手机和电脑版正确方法

如何将PDF转换成Excel?简单步骤解析

如何查看电脑日志?简单步骤与工具推荐

如何在PPT中插入背景图片?3步操作详解

微信能直接转账到支付宝吗?如何实现跨平台转账?

电脑锁屏如何设置?Windows与Mac系统操作步骤详解

如何打开MDF文件?推荐工具与操作步骤

如何将A4纸打印成一半大小?简单步骤解析

如何改变思维模式?有效方法与实用步骤

如何设置有效性规则,分步指南与最佳实践

微信如何换行打字?手机和电脑版正确方法

如何将PDF转换成Excel?简单步骤解析

如何查看电脑日志?简单步骤与工具推荐
